A Gentle Introduction to Formal Verification¶
Introduction¶
Most folks who come from a design or functional simulation background (UVM style verification) find Formal Verification intimidating. This typically happens because of:
- Lack of practice and unfamiliarity with writing assertions
- Verifying a block using Formal requires different techniques and a different mindset when compared to functional simulation
- A fear of signing-off on your block using Formal, i.e., how do you tell that you're done verifying a block when using Formal?
- At conferences you only hear Formal "experts" with Ph.Ds. talk about Formal so you feel it is a very difficult thing to learn
In this set of articles on Formal Verification my intention is to de-mystify all the above points and prove it to you that if you're a Designer or a DV engineer, Formal Verification is your new best friend. It is time to break the ice and get familiar with this new tool. Yes, it is hard at first, but once you get some practice with Formal Verification it'll come to you naturally and, like me, you'll enjoy it more than functional simulation. 🤘
But, this is where we start. This article is just a bunch of words, you won't be cracking any code here. So, sit back get yourself a hot cup of chai ☕ and read on. The intention here is to start by understanding 4 things
- The difference between Formal Verification and Functional Simulation?
- When should you use Formal Verification?
- The mindset required to do Formal
- The road to becoming an expert at Formal
Once you've made it through this article, proceed to read the following two articles:
Formal Verification vs Functional Simulation¶
Formal Verification (a.k.a Formal, a.k.a FV) is a different style of verification but achieves the same end goal -- weeding out bugs from your design. The testbench, constraints, checkers and coverage are written using SystemVerilog Assertions.
One of the big differences between Functional and Formal Verification is the role that the tool plays.
Functional Simulation¶
In a typical functional simulation, you write every piece of the testbench manually.
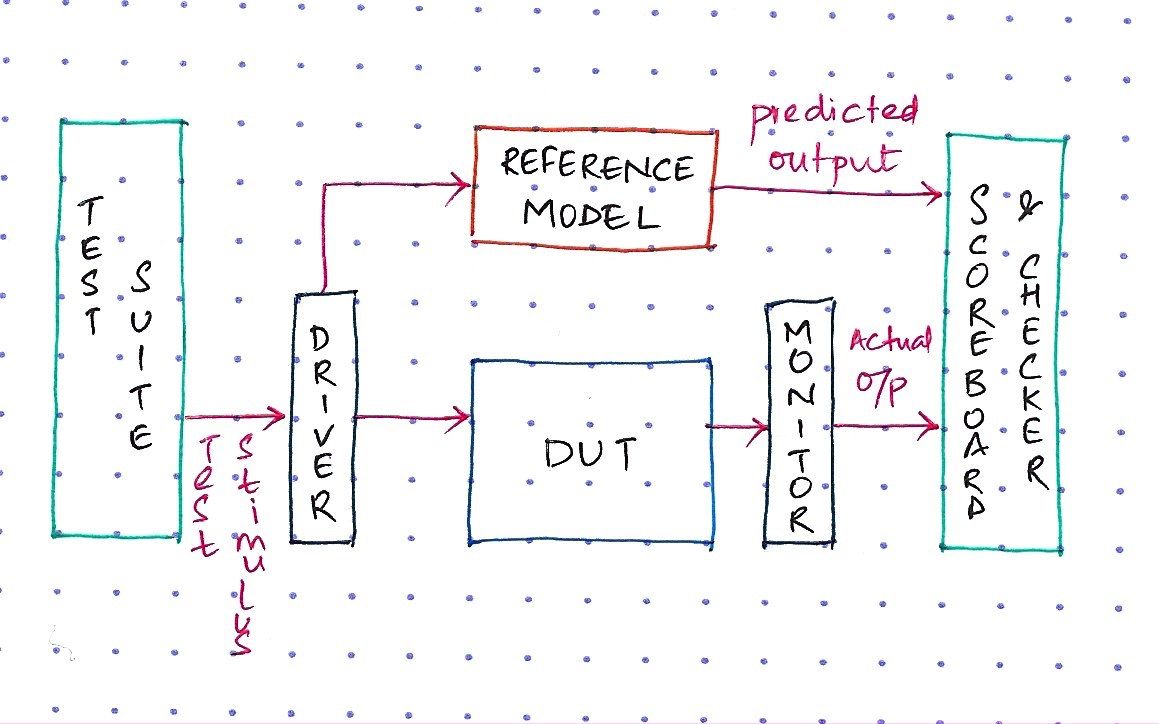
Testcase- You generate the stimulus and decide when it is injected into the RTLDriver- You write the drivers or BFMs that do the injection of the stimulus based on a certain protocolMonitor- You write the monitors that receive the output from the RTLModel- You code a detailed reference model, a zero-time equivalent of the RTL, which produces a predicted resultCheckers- You write the checkers and scoreboard that compare the output from the RTL versus that from your reference model and declare Pass or Fail
Yep, I think you get the point ... You do all the work. The testbench and tests orchestrate everything, and the tool merely simulates on a clock-by-clock basis what's happening in the RTL as you inject the desired stimulus. Also, a lot of code needs to be written before you can write your first test.
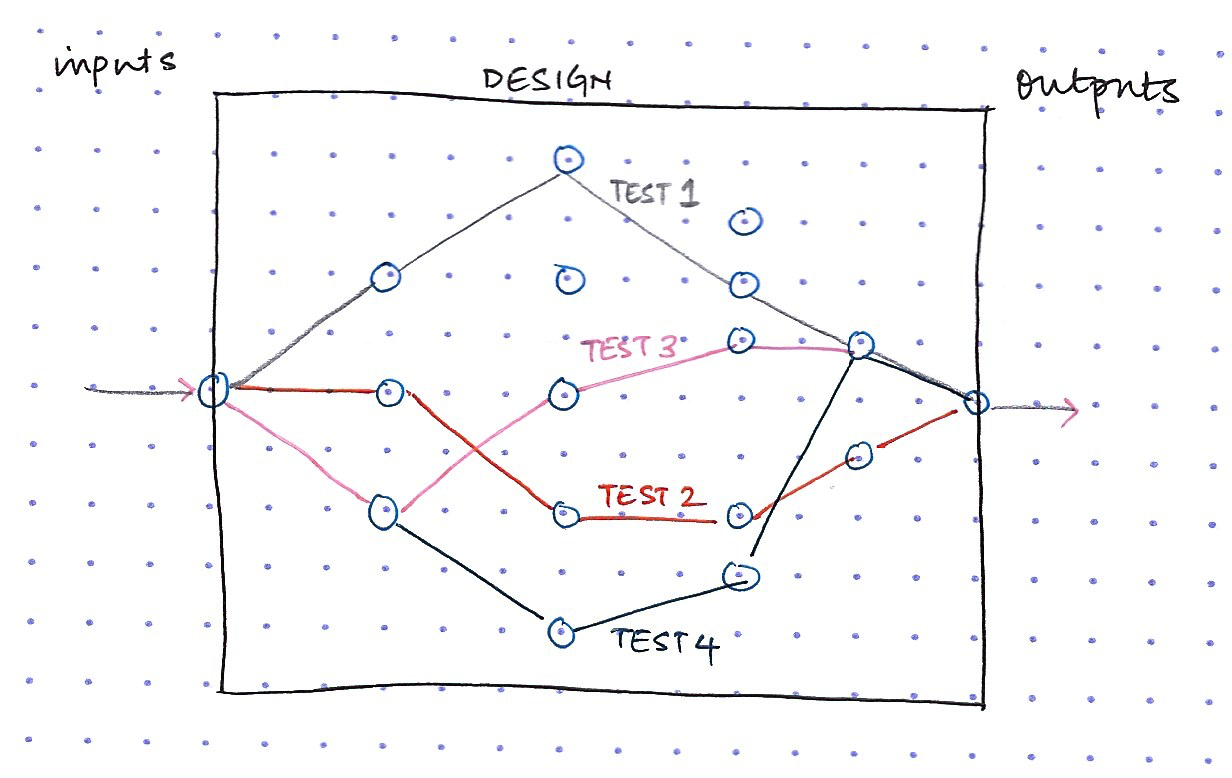
Another way to visualize this is, every testcase you write exercises a different code path in the DUT. In a constrained-random methodology you write a few tests and run them several times to cover different paths in the state space. But, the end result is the same -- in functional simulation every time you run a test a single specific code path is tested.
Formal Verification¶
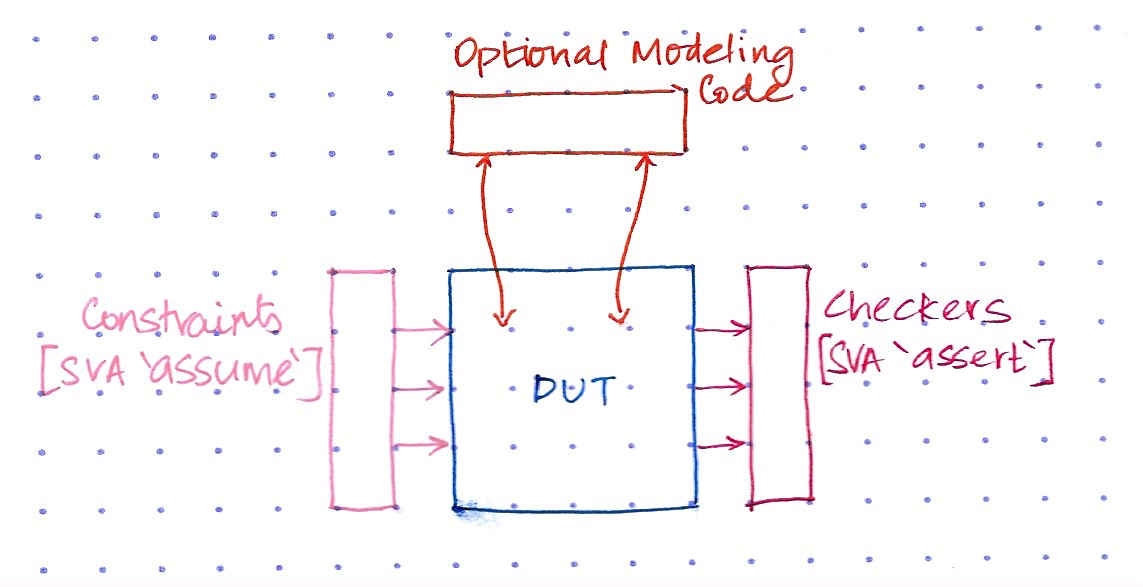
In Formal Verification, the tool does a lot of the heavy lifting. There is no concept of driver, monitor or test cases. Here,
- The inputs or internal variables of the DUT are constrainted according to the design specification using SVA
assumedirective - Checkers are written on the desired outputs, or internal variables of the DUT, using SVA
assertdirective - SVA cover property is used to collect functional coverage
- You could also write small pieces of modeling code which are just sufficient for a particular checker. This is different from Functional Simulation where you write a detailed reference model of the block you are verifying.
When you feed these constraints, checkers and the RTL to the Formal tool, it turns everything into mathematical equations.
What does this mean?
The DUT is essentially a network of logical gates and flip-flops. This network of gates & flops can be represented as equations. The tool then analyzes each checker (i.e., SVA assertion) independently and mathematically tries to seek out any sequence of inputs that could prove the checker false. If it does find such a sequence, then it provides a waveform showing this error scenario. In Formal speak, this waveform is called a Counter Example (cex).
What exactly does the tool do?
Now, assume you have a checker that looks like this
// If inputs req_type is ADD and uncor_err is 1, then
// err_cnt_incr flag goes high in the same clock and
// one clock later interrupt is flagged
property AddUncorErrCheck;
@(posedge clk) disable iff (rst)
((req_type == ADD) && uncor_err) |->
(err_cnt_incr ##1 intr);
endproperty
AddUncorErrCheck_A: assert property (AddUncorErrCheck);
The tool analyzes this checker and determines all the inputs, outputs and internal variables of the DUT that influence this checker. The result of this analysis is called the cone-of-influence [COI] and this is how it is computed -
Quote
Computing the variables contained in the cone of influence is straightforward. The tool begins by including the variables that directly occur in the property specification into the cone-of-influence set. Then for each variable contained in the cone-of-influence set, the tool will identify all variables that appear on the right-hand side of the RTL assignments to this variable and add the new variables to the COI variable set. This process is repeated until no new variables can be added to the set.
Chapter 8: Applied Formal Verification, Doug Perry & Harry Foster
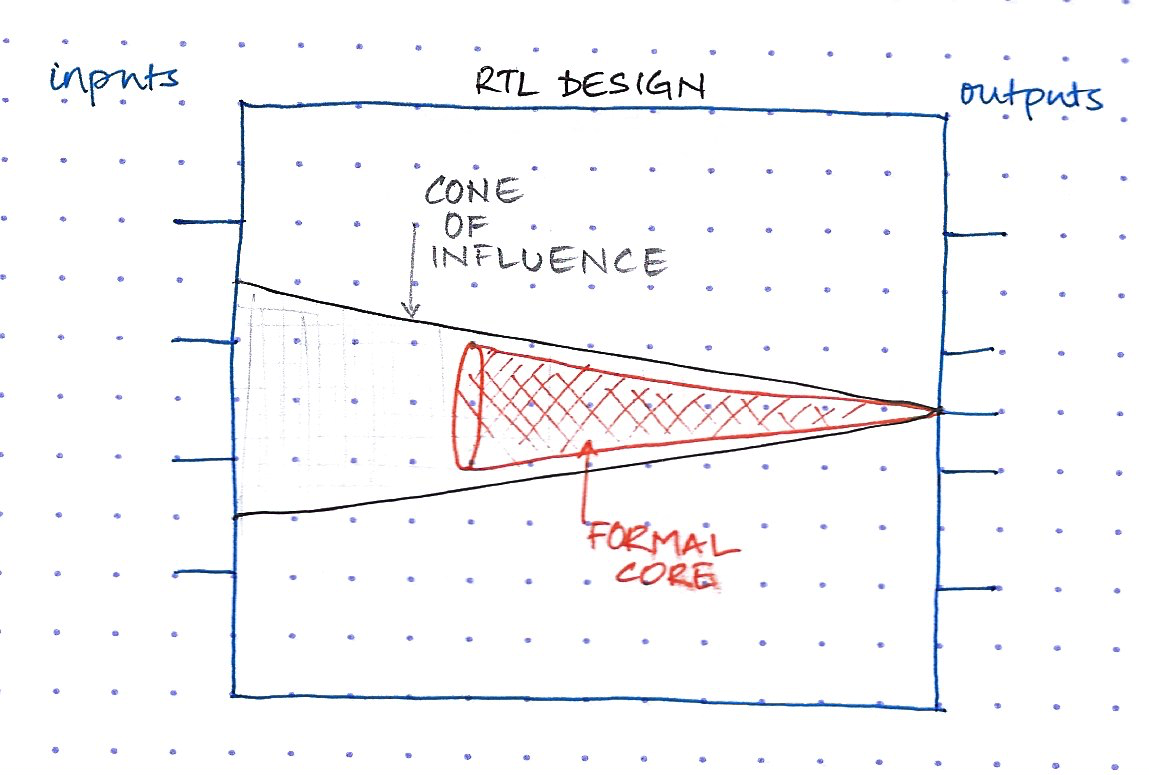
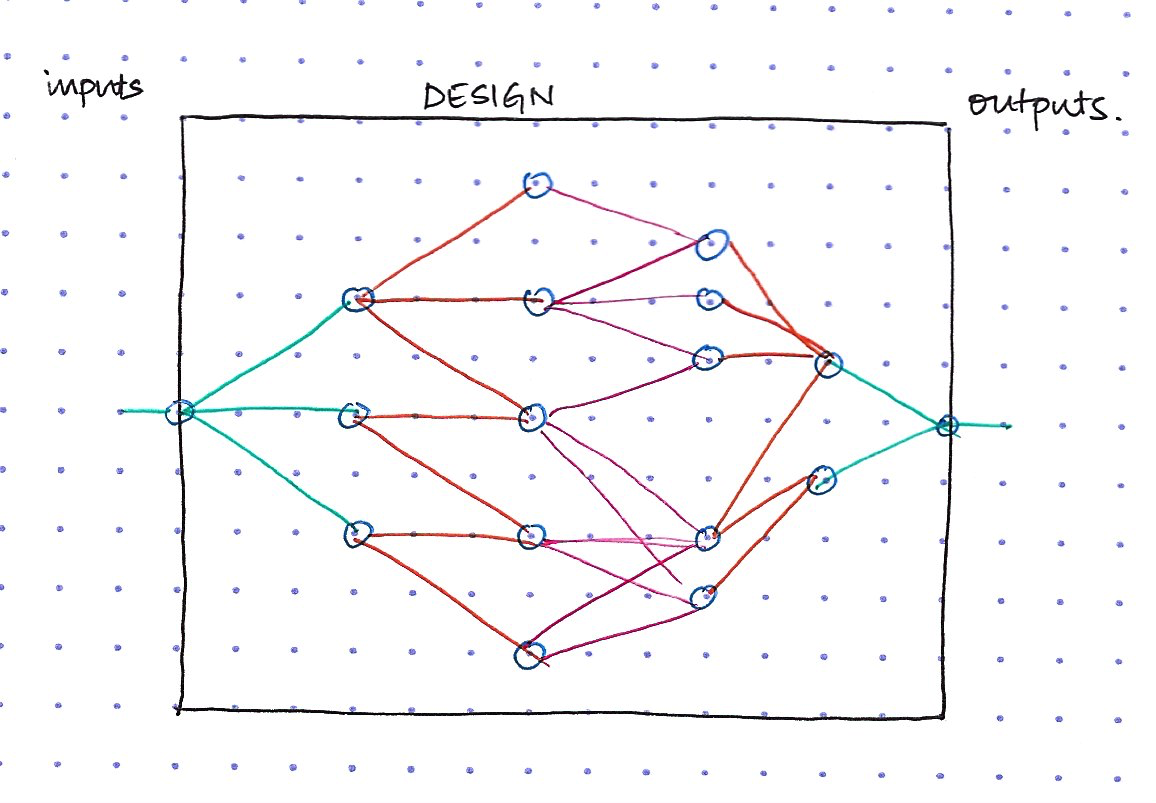
Once the cone of influence is determined, the tool can now determine the full state space of possible values the logic within the cone can take. It then parallelly explores every path in the state space (as shown in the diagram below) and checks if the assertion can be proven wrong.
In other words, you don't have to write testcases like you do in functional simulation. Once you constraint the inputs correctly and write checkers according to the design specification. The tool takes care of generating all stimulus and reporting back if there is a failure.
Note
Tools these days are quite clever, they further reduce the COI into something called a Formal Core, a subset of the COI, which is really the only thing that needs to be exercised in order to prove that your design obeys the checker.
When to use Formal¶
In a typical UVM verification strategy you have a top level testbench and a few sub-chip level testbenches that are created by partitioning the design. I like to think of Formal as a tool that can be use alongside a sub-chip UVM testbench.
I use two thumb rules to decide a suitable candidate for Formal Verification:
- Within a sub-chip if there's a piece of logic that is critical and complex such as a cache or an arbiter or a complex state machine, then I use Formal to just verify that critical module within the sub-chip.
- Within a module if there's a piece of code that makes the verification engineer nervous or if it keeps the designer up at night, then that module is a good candidate for some additional verification using Formal.
One of the bottle necks in Formal is the size of the design that you can feed to the tool. If the cone of influence is very large, i.e., if the state space of the Formal DUT is large, then the tool will not be able to converge and prove the checkers. Additionally, not all types of designs are suitable for Formal.
Becoming an Expert¶
In the last few years the best and most interesting papers presented at conferences such as DVCon and SNUG were from the Formal Verification track. So, the best way to improve your Formal chops is to read papers from previous conferences, and the best way to stay up-to-date with new Formal techniques, is to keep track of what your peers are doing with Formal, i.e., follow papers from future conferences.
That said, here is a list of resources which will help you learn.
Article:SystemVerilog Assertions BasicsArticle:A Blueprint for Formal VerificationTextbook:Formal Verification, Erik Seligman et. al. - This is the best resource available for FV. I constantly use this as a reference while I'm verifying a design. If you're serious about learning Formal, then purchase this textbook. Get yourself a highlighter and pencil, and study this textbook one chapter at a time. Make notes as your read it and re-read your notes and highlights at the end. Study it like you did while in University.Paper:Guidelines for Creating a Formal Verification Testplan - A good starting point before you begin verifying the design.Paper:Design Guidelines for Formal Verification - This is a good resource for design engineers on how to make their RTL Formal friendly.Paper:Sign-off with Bounded Formal Verification Proofs - In Formal, sooner or later you'll come across checkers that neither pass nor fail. Instead the tool reports them as Bounded Proofs. This happens when the tool can only prove the checkers to a specific cycle depth. This paper teaches you how to deal with Bounded Proofs.Textbook:Applied Formal Verification, Douglas Perry and Harry Foster - Another good resource that provides a simple introduction to FV.
As with learning anything new, it is important to immerse yourself into the subject and practice it intentionally.
- Spend time with the resources listed above and find ways to use Formal in your next verification cycle
- Start small, pick a single module, build a Formal testbench around it and write a few cover properties. The example I've shown in the previous section should be good enough to get you started.
- Run the tool and get familiar with the GUI as you run these cover props
- Next, write a simple assertion on one of the outputs and see it pass
- Change one of the above assertions to purposely make it incorrect (change an
==in the expression to a!=). Run this incorrect checker and observe the waveform that the tool shows you (this is also called the Counter Example). - Once you iterate over this a few times, you'll be ready to go to the next step, i.e., learn about Formal abstraction techniques and other good stuff
In a Nutshell¶
This is what we've established
- How Formal Verification is different from Functional Simulation
- What the Formal tool does when trying to prove an assertion
- When is Formal useful
- A list of resources to get you up and running with Formal Verification
Questions & Comments¶
For questions or comments on this article, please use the following link.

